正規分布とファットテール：なぜ金融市場の暴落は「想定外」に起きるのか

概論

金融の世界では、将来の不確実性を飼いならすため、様々な統計モデルが用いられてきました。その中でも、最も基本的で、かつ長年にわたり金融理論の根幹を支えてきたのが正規分布（Normal Distribution）、いわゆる「ベルカーブ」です。

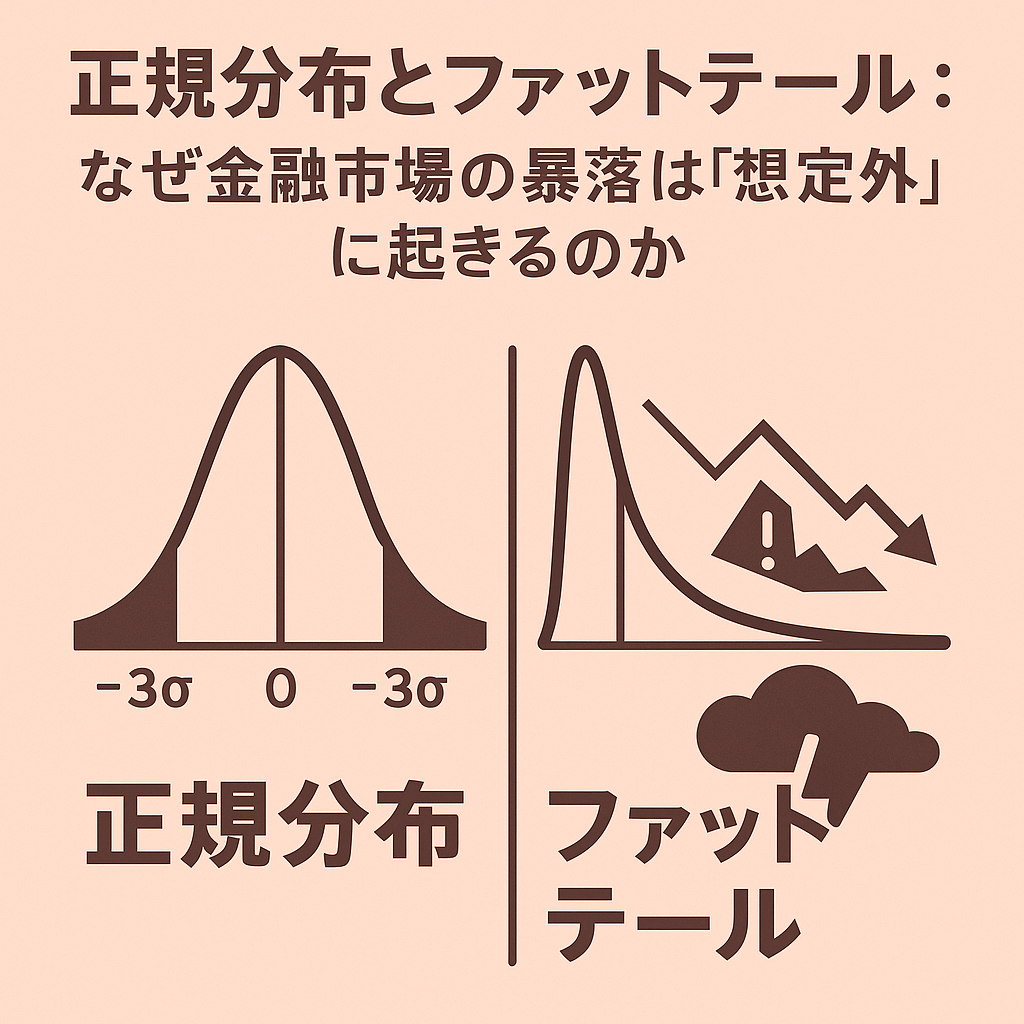
正規分布は、平均値を中心に左右対称の美しい釣鐘状を描き、平均から離れた極端な事象が起こる確率は、指数関数的に減少していきます。この「予測しやすさ」と「扱いやすさ」から、ハリー・マーコウィッツが1952年に提唱した現代ポートフォリオ理論をはじめ [1]、多くの伝統的な金融モデルは、資産のリターンが正規分布に従うことを暗黙の前提として構築されてきました。

しかし、現実の金融市場は、この理論が想定するほど穏やかで予測可能な世界ではありません。「100年に一度」と言われるような暴落が、なぜか10年に一度くらいの頻度で発生する。この理論と現実の残酷なギャップを生み出す根源こそが、ファットテール（Fat Tails）と呼ばれる現象です。

ファットテールとは、資産リターンの確率分布において、正規分布が予測するよりも、極端な事象（暴騰や暴落）が遥かに高い頻度で発生する性質を指します。分布のグラフを描いた際に、両裾（テール）の部分が、正規分布の裾よりも「太く（Fat）」なることから、このように呼ばれています。

この金融リターンの根源的な性質を学術的に初めて喝破したのが、数学者のブノワ・マンデルブロです。彼は1963年の論文で、綿花価格の変動が正規分布ではなく、裾が非常に厚い「安定パレート分布」に従うことを示しました [2]。その後、ユージン・ファーマも1965年の研究で、株式リターンが正規分布から大きく逸脱し、極端な変動が多い（専門的には「尖度が大きい」）ことを実証しました [3]。

これらの発見は、金融市場のリスクが、伝統的なモデルが想定していたよりも、遥かに危険で、予測困難であることを意味していました。

---

長短の解説、利益例・損失例の紹介

短所、弱み、リスクについて：正規分布モデルの致命的な欠陥

ファットテールの存在を無視し、正規分布を前提としたリスク管理を行うことは、壊れたコンパスを頼りに航海に出るようなものであり、壊滅的な損失に繋がる危険性をはらんでいます。

損失事例１：リスクの体系的な過小評価

正規分布を前提としたリスクモデル（例えば、伝統的なバリュー・アット・リスク、VaR）は、その構造上、市場が暴落する確率とその規模を、体系的に過小評価します。

モデル上では「標準偏差のマイナス5倍を超えるような下落（5シグマ・イベント）は、天文学的に低い確率でしか起こらない」と計算されても、現実のファットテールを持つ市場では、それが数年に一度の頻度で起こり得ます。このモデルへの盲信は、投資家に過剰なリスクを取らせ、本来備えるべきだったはずの「想定外」の損失に対して、全くの無防備な状態を晒させてしまうのです。

損失事例２：2008年世界金融危機

このモデルの欠陥が世界経済を揺るがす形で露呈したのが、2008年の世界金融危機です。

フィリップ・ジョリオンの2009年の分析によれば、多くの大手金融機関が用いていたリスク管理モデルは、正規分布の仮定に過度に依存していたため、サブプライムローン関連証券が持つ「テールリスク（稀だが巨大な損失が発生するリスク）」を完全に見過ごしていました [4]。モデルが「安全」だと判断した資産が、実際には経済全体を崩壊させる爆弾であったことが明らかになったのです。

長所、強み、有用な点について：ファットテールを前提としたアプローチ

ファットテールの存在は、リスク管理における深刻な課題であると同時に、それを認識し、適切に対応する投資家にとっては、新たな機会の源泉ともなり得ます。

利益例１：より現実に即したリスクモデルの構築

ファットテールという現実を直視することから、より洗練されたリスクモデルが生まれました。その代表例が、ティム・ボラースレフが1986年に提唱したGARCHモデルです [5]。

GARCHモデルは、金融市場に見られる「ボラティリティのクラスター性（変動が激しい時期は続き、穏やかな時期も続く）」という特徴を捉えることができます。この性質こそが、ファットテールを生み出す主要な原因の一つです。GARCHモデルのような、より現実に即したモデルを用いることで、投資家はリスクをより正確に把握し、急な市場変動に対する備えを固めることができます。

利益例２：行動ファイナンス的アプローチ

ファットテールは、単なる統計的な現象ではなく、しばしば人間の集団的な心理、すなわち「パニック売り」や「熱狂的なバブル」によって引き起こされます。

ニコラス・バーバリスによる2013年のレビュー論文でも論じられているように、プロスペクト理論などの行動ファイナンスの知見は、なぜ投資家が極端な事象に対して過剰に反応し、ファットテールを生み出してしまうのかを説明する上で、多くの示唆を与えてくれます [6]。テールリスクそのものを取引の対象とするテールリスク・ヘッジ戦略や、パニックによって生まれるトレンドを追随する戦略など、ファットテールを脅威として避けるだけでなく、その背後にある投資家心理を理解することで、それをエッジに変えようとするアプローチも存在します。
非対称性と摩擦の視点から

なぜ、金融市場は正規分布という穏やかな世界に従わず、ファットテールという暴力的な性質を示すのでしょうか。そして、なぜ多くの金融モデルは、その現実から目を背け続けてきたのでしょうか。その本質を、当メディアの根幹をなす「非対称性」と「摩擦」の観点から解き明かすことができます。

---

非対称性と摩擦の視点から

Asymmetry：正規分布とファットテールの「構造的」非対称性

正規分布と、現実の金融市場が示すファットテールの分布との間には、構造的な「非対称性」が存在します。

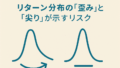
正規分布は、その名の通り、平均値を中心に完全に左右対称な形をしています。つまり、プラス方向への極端な動き（暴騰）と、マイナス方向への極端な動き（暴落）が、同じ確率で起こることを前提としています。

しかし、現実の市場はそうではありません。多くの場合、市場の暴落は、暴騰よりも遥かに短い期間で、より激しく起こります。つまり、リターン分布の左裾（マイナス側）は、右裾（プラス側）よりも太く、長くなる傾向があります。このリターン分布そのものが持つ「負の歪度（ネガティブ・スキュー）」という非対称性が、ファットテールの一因となります。

さらに、プロスペクト理論が示すように、投資家は利益と損失を非対称に評価します [6]。100万円の利益を得る喜びよりも、100万円の損失を被る苦痛の方が、精神的には遥かに大きいのです。この投資家心理の非対称性が、市場が下落局面に差し掛かった際に、パニック的な売りを誘発し、それがさらなる下落を呼ぶという負の連鎖を生み出し、正規分布が想定するよりも遥かに厚い、左側のファットテールを形成するのです。

---

Friction：モデルへの「固執」という認知的摩擦

手数料やスプレッドのような基本的な摩擦に加え、金融界が長年にわたりファットテールという現実を直視できなかった背景には、より根深い、認知的な摩擦が存在します。

数学的な「扱いやすさ」という摩擦

正規分布が金融モデルで広く使われてきた最大の理由は、その数学的な「扱いやすさ」にあります。正規分布は、平均と標準偏差という二つのパラメータだけで、その分布の全ての性質を記述できる、非常にエレガントなモデルです。

一方で、マンデルブロが提唱したような、ファットテールを正確に記述する分布モデルは、数学的に極めて複雑で、扱いが困難です [2]。この「モデルの複雑性」という摩擦が、多くの研究者や実務家を、不正確であることを知りながらも、より単純で扱いやすい正規分布のモデルに固執させる原因となってきました。

既存インフラという制度的摩擦

大手金融機関のリスク管理システムや、規制当局が定める自己資本比率の計算ルール、デリバティブの価格評価モデルなどは、その多くが正規分布の仮定を前提として、何十年もかけて構築されてきました。

ファットテールを本格的にモデルに組み込むことは、これらの巨大な既存インフラを根本から覆し、再構築することを意味します。その莫大なコストと、業界全体の慣行を変えることの難しさという「制度的な摩擦」が、より現実に即したリスクモデルへの移行を遅らせる大きな要因となってきたのです。2008年の金融危機は、この摩擦がもたらした悲劇的な帰結の一つと言えるでしょう [4]。

---

総括

・伝統的な金融理論の多くは、資産リターンが予測しやすい「正規分布」に従うことを前提としてきました [1]。

・しかし、現実の金融市場は、暴騰や暴落といった極端な事象が理論の想定を遥かに超えて頻繁に起こる「ファットテール」という性質を持っています [2, 3]。

・正規分布を前提としたリスク管理モデルは、このファットテールを無視するため、市場暴落のリスクを体系的に過小評価するという致命的な欠陥を抱えています。2008年の金融危機は、その代表的な失敗事例です [4]。

・ファットテールは、ボラティリティのクラスター性を捉えるGARCHモデル [5]や、行動ファイナンスの知見 [6]を取り入れることで、より現実的に理解・分析することが可能になります。

---

用語集

正規分布 (Normal Distribution) 統計学で最も広く用いられる確率分布の一つ。平均値を中心に左右対称の釣鐘状の形をしており、「ベルカーブ」とも呼ばれる。

ファットテール (Fat Tails) 確率分布において、平均から大きく離れた極端な事象（テールイベント）が、正規分布の予測よりも高い確率で発生する性質。

現代ポートフォリオ理論 (Modern Portfolio Theory) ハリー・マーコウィッツが提唱した、資産のリターンとリスク（分散）を基に、最も効率的なポートフォリオを構築するための理論。

尖度 (Kurtosis) 確率分布の「尖り具合」と「裾の厚さ」を示す統計的な指標。正規分布よりも裾が厚い（ファットテールを持つ）分布は、尖度が正の大きな値を取る。

歪度 (Skewness) 確率分布が、その平均値に対してどれだけ非対称であるかを示す指標。「負の歪度」が大きいとは、分布の裾が左側（マイナス側）に長く伸びていることを意味する。

バリュー・アット・リスク (VaR) ある一定期間において、特定の確率で発生しうる最大の損失額を推計したリスク指標。伝統的なVaRモデルは正規分布を仮定することが多い。

テールリスク (Tail Risk) 確率分布の裾（テール）の部分で発生する、確率は低いが、一度発生すると極めて甚大な損失をもたらすリスク。

ボラティリティ・クラスタリング (Volatility Clustering) 金融市場において、価格変動が激しい時期（高ボラティリティ）としばらく続き、価格変動が穏やかな時期（低ボラティリティ）もしばらく続くという、変動率の性質。

GARCHモデル ボラティリティ・クラスタリングを統計的にモデル化する手法の一つ。ファットテールを持つ金融時系列データの分析に広く用いられる。

プロスペクト理論 不確実性のある状況下での人間の意思決定を説明する理論。損失を重く感じる、低い確率を過大評価するなど、人間の認知バイアスをモデル化している。

---

参考文献一覧

[1] Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91.
https://doi.org/10.2307/2975974

[2] Mandelbrot, B. (1963). The variation of certain speculative prices. The Journal of Business, 36(4), 394-419.
https://doi.org/10.1086/294632

[3] Fama, E. F. (1965). The behavior of stock-market prices. The Journal of Business, 38(1), 34-105.
https://doi.org/10.1086/294743

[4] Jorion, P. (2009). Risk management lessons from the credit crisis. European Financial Management, 15(5), 923-933.
https://doi.org/10.1111/j.1468-036X.2009.00507.x

[5] Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 31(3), 307-327.
https://doi.org/10.1016/0304-4076(86)90063-1

[6] Barberis, N. (2013). Thirty years of prospect theory in economics: A review and assessment. Journal of Economic Perspectives, 27(1), 173-96.
https://doi.org/10.1257/jep.27.1.173