金融という本質的に「不確実性」を内包する世界の中で、将来起こりうる無数のシナリオを描き出し、リスクを測定し、複雑な金融商品の価値を評価するための最も強力なアプローチの一つがモンテカルロ・シミュレーション(Monte Carlo Simulation, 以下MCS)です。
この記事は、MCSを自ら実装し、その結果を解釈・評価する際に必要となる「戦略的な思考法」を身につけるためのガイドです。具体的なコードではなく、その背後にあるモデル設計の思想、結果の妥当性を見抜くための視点、そして避けるべき落とし穴に焦点を当てて解説します。
第1章 モンテカルロ・シミュレーションとは何か?
1-1. 本質は「多数の“もしも”を計算し、未来の姿を浮かび上がらせること」
MCSを一言で表すなら、「ランダムな事象(乱数)を大量に発生させ、それに基づいたシミュレーションを何度も繰り返すことで、確率的にしか分からない問題の近似解を求める統計的手法」です。
例えば、非常に複雑な形をした池の面積を知りたいとします。数式で計算するのは困難です。そこで、まずその池を完全に囲む正方形の土地を用意し、その土地に向かってランダムに大量の石を投げ込みます。最終的に、正方形の土地全体に落ちた石の総数と、そのうち池の中に着水した石の数の比率を計算すれば、正方形の面積に対する池の面積の割合をかなり正確に推定できます。
この石投げのアナロジーが、MCSの本質を的確に捉えています。金融の世界では、「石」が将来の株価や金利といったランダムに変動する変数であり、「池」が利益や損失といった評価したい対象です。コンピュータ上で何万、何十万通りもの「あり得たかもしれない未来」を擬似的に生成することで、私たちはその結果の分布や平均的な姿を統計的に把握するのです。
1-2. なぜ金融の世界で不可欠なのか
MCSは、解析解が存在しない複雑な問題に対して、極めて強力な解決策を提供します。将来の不確実な要因(株価、金利など)の変動シナリオを多数シミュレートし、それぞれのシナリオから得られる結果(オプションの価値、ポートフォリオの損益など)の平均値を計算することで、近似的な解を導き出すのです。
1-3. 収束と精度:知っておくべき基本特性
MCSの推定誤差は、試行回数 N に対し、おおむね
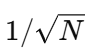
のオーダーで減少します。これは「精度を10倍にするには、試行回数を100倍にする必要がある」ことを意味します。この計算コストの問題を克服するために、「バリアンス低減法」という統計的なテクニックが極めて重要になります(第5章で詳述)。
第2章 金融における主要ユースケース
MCSの柔軟性と拡張性は、金融の様々な分野でその価値を発揮します。
- デリバティブ価格評価 将来の資産価格の経路に依存する(パス依存型)オプションなど、複雑なデリバティブの価格評価はMCSの独擅場です。
- マーケットリスク管理 金融機関が保有するポートフォリオのリスクを測る代表的な指標、バリュー・アット・リスク (Value-at-Risk, VaR)や期待ショートフォール (Expected Shortfall, ES) の算出に広く用いられます。
- 信用リスク評価 複数の企業が同時にデフォルト(債務不履行)する相関をモデル化するため、コピュラ理論をMCSに組み込むことで、ポートフォリオが抱える信用リスクを評価します。
- 資産負債管理 (ALM) 銀行や保険会社が、将来の金利や株価の長期的なパスをシミュレートし、財務健全性(ソルベンシー)や流動性を評価するために活用します。
第3章 信頼できるシミュレーションの設計:実務チェックリスト
この章では、シミュレーションの信頼性を根幹から支えるモデル設計上の重要ポイントを、実務的なチェックリストとして解説します。「Garbage In, Garbage Out」を避けるための、設計思想の核心部分です。
- 分布の選択:正規分布を疑う 多くの金融理論の出発点である正規分布は、現実の市場が持つ「裾の厚さ(ファット・テール)」や「歪度(分布の非対称性)」を捉えきれません。t分布や混合正規分布など、テールリスクを表現できる分布の採用を常に検討すべきです。
- 相関構造:静的な相関は危険 平時の市場では緩やかに相関している資産が、市場のストレス時には一斉に下落します。単純な相関係数だけでは、このような非線形な依存関係や、時間と共に変化する相関構造を捉えることはできません。コピュラ理論やDCC-GARCHモデルなど、より高度な相関モデリングの導入が必要か検討します。
- 測度の選択:リスク中立測度 vs 実世界測度 これは実務上、最も混同しやすく、かつ致命的な誤りを生むポイントです。
- リスク中立測度: デリバティブの価格評価で用います。
- 実世界測度: VaRの計算など、将来の損益分布を予測するリスク管理で用います。
- 時間離散化の誤差管理 連続時間モデルをシミュレーションする際、時間を微小なステップに区切りますが、このステップ幅が大きいと離散化誤差が生じます。ミルシュタイン・スキームのような、より高次の近似手法の採用も検討する必要があります。
- 現実世界の制約を反映させる 理論モデルだけでは不十分です。証拠金制度、取引コスト、規制(バーゼル合意など)、会計基準といった、現実の制度や制約をモデルに組み込むことで、初めてシミュレーションは実務的な価値を持ちます。
第4章 シミュレーションのエンジン:乱数生成と相関の付与
4-1. 乱数生成
シミュレーションの出発点は、コンピュータによる乱数の生成です。通常、一様乱数を生成し、それを逆関数法などの手法で様々な確率分布に従う乱数に変換します。実務では、結果の再現性を確保するために、乱数生成の出発点となるシード(種)を固定することが不可欠です。
4-2. 多変量正規分布とコレスキー分解
複数の資産を扱う場合、資産間の相関も考慮する必要があります。各資産のリターンが多変量正規分布に従うと仮定した場合、コレスキー分解が有効です。これは、資産間の相関情報をまとめた共分散行列 (Σ) を用いて、望ましい相関構造を持つ乱数ベクトルを生成する手法です。
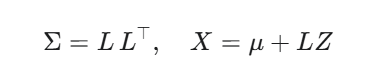
4-3. 非正規分布の相関:コピュラ理論
各資産のリターンが正規分布に従わない場合、コレスキー分解は使えません。ここで登場するのがコピュラ理論です。コピュラは、多変量分布を「各変数の周辺分布(分布の形状)」と「変数間の依存構造(相関)」に分離するための数学的な道具であり、これにより、非常に柔軟なモデリングが可能になります。
第5章 計算の高速化・高精度化:バリアンス低減と準モンテカルロ
この章では、計算コストを抑えつつ、より少ない試行回数で精度の高い結果を得るための統計的テクニックを解説します。これらを使いこなすことが、MCSを実務の現場で現実的なツールにする鍵となります。
- 反対変量法 (Antithetic Variates) 標準正規乱数 (Z) を生成した際、同時にその符号を反転させた (−Z) も利用する手法です。両者から生成された結果の平均を取ると、ばらつきが相殺され、分散が小さくなる傾向があります。
- 制御変量法 (Control Variates) 求めたい値と相関が高く、かつ解析解が分かっている単純な変数を「制御変量」として利用し、シミュレーション結果を補正することで分散を縮小させます。
- 層化抽出法 (Stratified Sampling) 乱数を生成する確率空間全体を、いくつかの重複しないグループ(層)に分割し、各グループからバランス良くサンプルを抽出する手法です。
- 重要度サンプリング (Importance Sampling) 特にテールリスクの評価など、発生確率が低いが結果に重大な影響を与える事象を評価する際に威力を発揮します。
- 準モンテカルロ法 (Quasi-Monte Carlo, QMC) これは、ランダムな乱数列の代わりに、低食い違い量列(Low-Discrepancy Sequence) と呼ばれる、より均一に空間を埋め尽くすように設計された数列を用いる手法です。Sobol列やHalton列が有名で、低〜中次元では経験的にMCより速い収束を示し、O((logN)d/N) に近い挙動が観察されることもあります。
第6章 実装の思考プロセス(1):オプション価格評価の例
具体的なコードの代わりに、ヨーロピアン・オプションの価格評価をMCSで実行する際の「思考の青写真」を示します。
1.モデルの特定: まず、価格評価の土台となる数理モデルを決定します。デリバティブ価格評価の標準的な出発点は、リスク中立測度の下での幾何ブラウン運動モデルです。
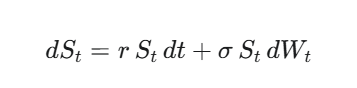
2.解析解の導出: このモデルから、満期 T における株価 ST の分布を数式で導きます。
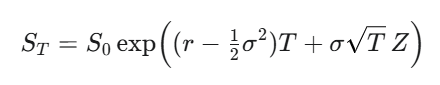
ここで Z は標準正規分布に従う確率変数です。
3.シミュレーション設計:
- 乱数生成器の選択: 標準正規乱数 Z を生成します。精度を高めるため、ここでは準モンテカルロ法(Sobol列)を選択するのが定石です。
- 効率化手法の選択: 計算効率をさらに高めるため、反対変量法を組み合わせます。これにより、実質的なサンプル数を増やし、推定値の分散を低減させます。
- パス生成: 生成した多数の乱数 Z を上記の ST の式に代入し、何万通りもの満期株価のシナリオを生成します。
4.ペイオフ計算と集計:
- 各シナリオの満期株価 ST について、オプションのペイオフ(利益)を計算します(コールオプションなら max(ST − K,0))。
- 全シナリオのペイオフの平均値を算出します。
- 最後に、その平均値をリスクフリーレート r で満期 T から現在まで割り引きます。これがMCSによるオプション価格の推定値となります。
5.不確実性の評価: 推定値はあくまで統計的な近似値です。その信頼性を示すため、信頼区間(CI)を必ず併記する必要があります。これは、シミュレーションを複数回(レプリカ)実行し、得られた複数の推定値のばらつきから標準誤差(SE)を計算することで求められます。
第7章 実装の思考プロセス(2):ポートフォリオのリスク計測
次に、ポートフォリオのVaRやESを計測する際の思考プロセスを解説します。
- リスクモデルの特定: 将来の損益分布を予測するため、実世界測度の下でのリターンモデルを定義します。ここでは、複数の資産リターンが多変量正規分布に従うと仮定します。このモデルは、各資産の期待リターンベクトル (μ) と、資産間の相関を含む共分散行列 (Σ) によって特徴づけられます。
- シミュレーション設計:
- 相関乱数の生成: ポートフォリオのリスクは資産間の相関に大きく依存します。共分散行列 (Σ) をコレスキー分解し、無相関な正規乱数から、望ましい相関構造を持つ多変量正規乱数を生成します。
- シナリオ生成: 生成した多数のリターンシナリオ (R) を基に、ポートフォリオ全体の損益(P&L)シナリオを計算します。
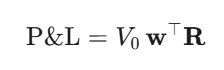
- リスク指標の算出:
- 計算された何万通りものP&Lシナリオを、損失の大きい順に並べます。
- VaR: 損失分布の99パーセンタイルなど、特定の分位点を読み取ります。これが「99%の確率で損失はこれ以内収まる」という閾値になります。
- ES: そのVaRの閾値を超えた損失シナリオだけを取り出し、その平均値を計算します。これが「万が一VaRを超えた場合に想定される平均的な損失額」です。
- 不確実性の評価と安定性: VaRやESといったテール指標は、シミュレーションのばらつきの影響を受けやすいです。そのため、算出された値自体の信頼性を評価することが重要です。ブートストラップ法などの統計手法を用いて、VaRやESの信頼区間を推定し、結果の安定性を確認します。
第8章 信頼性の担保:検証とレポーティング
モデルを構築し、結果を出すだけでは不十分です。その結果が信頼に足るものであることを、客観的に示さなければなりません。
- ベンチマークとの比較 可能な限り、解析解や他の高精度な数値解、既存のモデルと比較検証します。価格の差だけでなく、グリークス(価格の感応度指標)の差や、生成された分布のモーメント(平均、分散、歪度、尖度)が妥当であるかを確認します。
- 統計的精度の明記 経営層や顧客、監査部門への報告では、推定値そのものだけでなく、標準誤差や信頼区間を必ず併記します。これにより、シミュレーション結果が持つ本質的な不確実性を透明に伝えることができます。
- 感度分析とストレスシナリオ 入力パラメータ(ボラティリティ、相関など)がわずかに変化した際に、結果がどの程度変動するか(感度分析)を評価します。また、「相関が崩壊する」「流動性が枯渇する」といった、モデルの前提が崩れるような極端なストレスシナリオに対する頑健性も検証します。
- バックテスト VaRの文脈では、算出されたVaRが信頼できるかを検証するため、過去のデータを用いて、実際にVaRを超える損失が発生した頻度が想定通り(例:1%)であったかを検証するバックテストが不可欠です。
- 監査証跡 (Audit Trail) の確保 「いつ、誰が、どのデータとコード、どのバージョン、どのシードを使って実行した結果か」 を完全に再現可能にしておくことは、ガバナンス上、極めて重要です。
第9章 よくある落とし穴とその回避策
MCSはその自由度の高さ故に、誤った使い方をされやすいツールでもあります。ここでは代表的な落とし穴を解説します。
- 落とし穴1:測度の取り違え 前述の通り、価格評価で実世界測度のドリフトを使ったり、VaR計算でリスク中立ドリフトを使ったりするミスです。
回避策:コードレビューの際、ドリフト項の定義が目的に合っているかを最優先で確認する文化を徹底します。 - 落とし穴2:静的な相関への過信 平時のデータから推定された相関は、金融危機の際には機能しません。ストレス局面では、多くの資産クラスの相関が
1に近づく形で急上昇し、非線形化します。
回避策:t-コピュラの導入や、過去のストレス局面のデータを用いたシナリオ分析を併用します。 - 落とし穴3:テールリスクの軽視 正規分布を安易に仮定することで、極端なイベント(テールイベント)の発生確率を著しく低く見積もってしまいます。
回避策:t分布や混合分布の採用、重要度サンプリングやQMCによってテールのサンプリング効率を向上させます。 - 落とし穴4:計算資源の無駄遣い Pythonでシミュレーションを実装する際、
forループを多用すると、処理速度がボトルネックになりがちです。
回避策:NumPyやNumbaライブラリを活用し、計算を可能な限りベクトル化します。大規模な計算では、GPU(PyTorch/JAX)や分散コンピューティング(Ray, Dask)の利用も視野に入れます。
第10章 まとめ:MCSを真の武器とするために
モンテカルロ・シミュレーションは、その「柔軟性 × 拡張性」こそが最大の武器です。コードを一行も書かなくとも、その戦略的思考を理解することは、現代の金融実務家にとって不可欠なスキルです。
- 現実を正しく捉えるモデルを設計し
- バリアンス低減やQMCといった効率化の概念を理解し
- 信頼区間と徹底的な検証でアウトプットの品質を見抜く
この3つの原則を身につけることで、MCSは単なるブラックボックスから、不確実な未来の意思決定を支える強力な羅針盤へと変わるでしょう。
モンテカルロシミュレーションのためのとても詳しい用語集
モンテカルロ法に関する用語は多数あります。これから学んでいく方のためにも、徹底的にまとめました。
あ行
- ALM (資産負債管理, Asset Liability Management) 銀行や保険会社などが、金利などの市場変動に対して資産と負債のバランスを統合的に管理する手法。MCSは、将来の金利パスなどをシミュレートするために用いられます 。
- アメリカン・オプション (American Option) 満期日までのいつでも権利行使が可能なオプション取引のことです 。各時点で権利行使すべきか待つべきかの最適判断が必要なため、価格評価が複雑になります 。
- 歪度 (Skewness) 確率分布の非対称性を示す指標。現実の資産リターン分布は左右対称な正規分布とは限らず、歪みを持っている場合があります 。
- 期待ショートフォール (Expected Shortfall, ES) VaRが示す最大損失額を、さらに超えてしまった場合に想定される平均的な損失額のことです 。VaRを補完するテールリスク指標として用いられます 。
- 期待値 (Expected Value) 確率的な事象において、試行を重ねたときに得られる結果の平均値のことです。サイコロを1回振ったときの目の期待値は3.5です 。
- 逆関数法 (Inverse Transform Method) 一様乱数を、目的の確率分布に従う乱数に変換するための基本的な手法の一つです 。
- 幾何ブラウン運動 (Geometric Brownian Motion) オプション価格評価において、リスク中立測度の下での株価の動きを記述するためによく用いられる確率過程モデルです 。
- グリークス (Greeks) デリバティブ価格の各リスク要因(原資産価格、ボラティリティなど)に対する感応度のことです 。
- クローズド・フォーム (Closed-form Solution) 「解析解」とほぼ同義。四則演算や指数関数、対数関数など、有限回の基本的な演算で表現できる数式解のことです。MCSは、このような解が存在しない問題で特に有効です 。
- 原資産 (Underlying Asset) オプション取引などのデリバティブの価値の源泉となる資産(株価など)のことです 。
- 現在価値 (Present Value) 将来のキャッシュフローを、金利などを考慮して現在の価値に割り引いたものです。オプション価格評価では、将来のペイオフの期待値を現在価値に割り引くことで価格を算出します 。
- コレスキー分解 (Cholesky Decomposition) 多変量正規分布に従う相関のある乱数を生成する際に用いられる行列分解の手法です 。資産間の相関情報が詰まった共分散行列を分解することで、相関を付与した乱数を効率的に生成できます 。
- コピュラ (Copula) 多変量分布を、「各変数の周辺分布(分布の形状)」と「変数間の依存構造(相関)」に分離するための数学的な道具です 。これにより、正規分布に従わない資産間の複雑な相関構造もモデル化できます 。
さ行
- GARCHモデル (GARCH Model) 資産リターンのボラティリティが時間と共に変動する(クラスタリングする)性質を捉えるための時系列モデルです 。
- 準モンテカルロ法 (Quasi-Monte Carlo, QMC) 通常の乱数列の代わりに、より均一に空間を埋め尽くすように設計された「低偏差列」(Sobol列など)を用いる手法です 。
- 信頼区間 (Confidence Interval, CI) 統計的な推定値が、どの程度の信頼性を持つかを示す範囲のことです 。MCSの結果を報告する際は、推定値の不確実性を明確にするため、信頼区間を併記することが推奨されます 。
- 標準誤差 (Standard Error, SE) 推定量のばらつきの大きさを示す指標で、推定値の精度の尺度となります 。試行回数 (N) の平方根に反比例します 。
- 標準偏差 (Standard Deviation) データのばらつきの大きさを測る代表的な指標。金融の世界では、資産価格の変動の大きさ(リスク)を示すためにボラティリティと同義で使われることが多いです 。
- 裾の厚さ (Kurtosis) 確率分布の尖り具合や裾の重さを示す指標。「ファット・テール」を持つ分布は、正規分布よりも裾が厚くなります 。
- 層化抽出法 (Stratified Sampling) 分散減少法の一種です 。起こりうる結果の全範囲をいくつかのグループ(層)に分け、各グループからバランス良くサンプルを抽出することで、全体のばらつきを抑え、推定の精度を高める手法です 。
た行
- テールリスク (Tail Risk) 確率分布の裾(テール)の部分で発生する、起こる確率は低いものの発生した場合の損失が非常に大きいリスクのことです 。
- デリバティブ (Derivative) 株式や債券などの原資産から派生した金融商品の総称。オプションや先物などが含まれます 。
- 低偏差列 (Low-Discrepancy Sequence) 準モンテカルロ法で用いられる、ランダムではなく、空間を均一に埋め尽くすように設計された数列のことです 。Sobol列やHalton列が代表的です 。
- 離散化誤差 (Discretization Error) 連続時間で変動する資産価格などを、シミュレーションのために微小な時間ステップに区切って(離散化して)計算する際に生じる誤差のことです 。
- ドリフト (Drift) 確率過程における、資産価格の平均的な変動(トレンド)部分のことです。価格評価ではリスク中立ドリフトを、リスク管理では実世界ドリフトを用います 。
な行
- NPV (正味現在価値, Net Present Value) プロジェクトなどが将来生み出すキャッシュフローの現在価値から、初期投資額を差し引いたものです。MCSは、キャッシュフローの不確実性を考慮したNPVの分布を評価するのに用いられます 。
- 乱数 (Random Number) サイコロの目のように、出現が予測できず、規則性なくランダムに現れる数のことです 。モンテカルロシミュレーションの根幹をなす要素です 。
は行
- バックテスト (Backtesting) 算出されたVaRの信頼性を検証するプロセスです 。過去のデータを用いて、実際にVaRを超える損失が発生した頻度が、想定された確率(例:1%)と整合的であったかを確認します 。
- バリュー・アット・リスク (Value-at-Risk, VaR) 「ある一定期間において、特定の確率で発生しうる最大損失額」を示すリスク指標です 。
- パス依存型 (Path-Dependent) 金融商品の価値が、満期時点の価格だけでなく、そこに至るまでの価格の経路(パス)に依存する性質のことです 。
- パスワイズ法 (Pathwise Method) モンテカルロ法を用いてグリークスを推定する手法の一つです 。
- 反対変量法 (Anthetic Variates) 分散減少法の一種です 。正規乱数 (Z) を生成した際に、同時にその符号を反転させた (-Z) もペアで利用することで、結果のばらつきを相殺し、推定の分散を減少させる手法です 。
- ファット・テール (Fat Tail) 確率分布の裾の部分が、正規分布に比べて厚くなっている性質のことです 。これは、極端な事象(市場の暴騰や暴落など)が、正規分布の仮定よりも高い頻度で起こることを意味します 。
- 複利計算 (Compound Interest Calculation) リターンが毎年一定であるという非現実的な仮定に基づいた計算方法。市場の変動を考慮できるMCSは、より現実的な資産予測を可能にします 。
- ブラック・ショールズ式 (Black-Scholes Formula) 特定の仮定のもとで、ヨーロピアン・オプションの理論価格を解析的に求めることができる数式です 。
- ブラック・スワン (Black Swan) 過去の経験則からは予測できず、発生した場合に極めて大きな衝撃をもたらす事象のことです 。MCSは過去のデータに基づくため、このような未知の事象を予測することは困難です 。
- ブートストラップ法 (Bootstrap Method) シミュレーションで得られた結果から、さらにランダムに再サンプリングを繰り返すことで、推定量の信頼区間を算出する統計的手法です 。
- 分散減少法 (Variance Reduction Method) モンテカルロシミュレーションにおいて、より少ない試行回数で、より精度の高い(結果のばらつきが小さい)推定値を得るための統計的なテクニックの総称です 。
- ペイオフ (Payoff) オプション取引において、満期日に得られる利益のことです 。
- Hestonモデル (Heston Model) ボラティリティ自体が確率的に変動する「確率的ボラティリティ」を考慮したオプション価格評価モデルの一つです 。
- Box–Muller法 (Box-Muller Transform) 一様乱数から正規乱数を生成するための変換手法の一つです 。
- ポートフォリオ (Portfolio) 投資家が保有する株式、債券、不動産などの金融資産の組み合わせのことです。
- ボラティリティ (Volatility) 資産価格の変動の激しさを示す指標のことです。一般的に、標準偏差で測定されます 。
ま行
- Mertonモデル (Merton Model) 資産価格が連続的な変動(ブラウン運動)だけでなく、突発的なジャンプ(価格の不連続な変化)を起こすことを考慮したモデルです 。
- モデルリスク (Model Risk) 価格評価やリスク計算に用いる数理モデルが、不完全であったり、現実を正しく捉えられていなかったりすることによって生じるリスクのことです 。
や行
- ヨーロピアン・オプション (European Option) 満期日にのみ権利行使が可能なオプション取引のことです 。
ら行
- リスク許容度 (Risk Tolerance) 投資家が、資産運用を行う上でどの程度の不確実性(リスク)を受け入れられるかを示す度合いのことです。
- リスク中立測度 (Risk-Neutral Measure) デリバティブの価格評価に用いられる、架空の世界の確率測度のことです 。この世界では、すべての資産の期待収益率が、安全資産利子率(リスクフリーレート)と等しくなるように調整されています 。
- 実世界測度 (Real-World Measure) VaRの計算など、将来の損益分布を予測するリスク管理で用いられる、現実世界の確率測度のことです 。投資家のリスク選好などを反映した、実際に期待される収益率(ドリフト)を含みます 。
- ロングスタッフ–シュワルツ法 (Longstaff-Schwartz Method, LSM) アメリカン・オプションの価格評価で用いられる近似解法の一つ 。シミュレーションと回帰分析を組み合わせ、各時点での最適な権利行使戦略を近似します 。
推奨読書
より深く理論を学びたい方のために、以下の専門書を推奨します。
- Glasserman, P. (2003). Monte Carlo Methods in Financial Engineering. Springer.
- McNeil, A. J., Frey, R., & Embrechts, P. (2015). Quantitative Risk Management. Princeton University Press.
- Owen, A. B. (2013). Monte Carlo theory, methods and examples.



コメント